Making Multiple Representations in Math with Digital Tools

Let’s be clear counting in small quantities is a skill most kids do naturally without much prompting or coaching needed, in fact the region of the brain we use for counting includes the same portion of the brain that controls our fingers. Research suggests this may be attributed to the fact that our ancestors first experience with numbers involved the fingers (Devlin, 2000). However counting and calculations that go beyond our friendly finger tips are likely to result in errors.
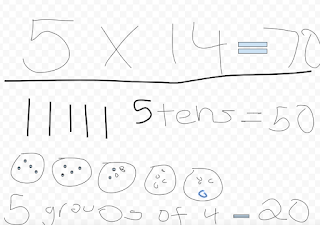 When it comes to calculations students need strategies and not just one. Research suggests students will most likely use a particular strategy that they find to be a more efficient solution for a particular type of problem (Sieger & Jenkinds, 1989). Take for example the problem 6 x 42 . Students who have proficiency with breaking apart numbers can determine they will need to calculate 6 X 40 (240) and 6 X 2 (12) and mentally calculate the total of 252, but when these numbers become much larger 656 X 3245 the standard algorithm becomes more efficient.
When it comes to calculations students need strategies and not just one. Research suggests students will most likely use a particular strategy that they find to be a more efficient solution for a particular type of problem (Sieger & Jenkinds, 1989). Take for example the problem 6 x 42 . Students who have proficiency with breaking apart numbers can determine they will need to calculate 6 X 40 (240) and 6 X 2 (12) and mentally calculate the total of 252, but when these numbers become much larger 656 X 3245 the standard algorithm becomes more efficient.
Common core mathematics shifts the focus from learning one-way and one-algorithm to understanding the underlying principles of a concept and applying multiple algorithms. This approach certainly lends itself to going deeper with math through multiple representations and ways of showing what you know.
The idea that students don’t begin with the end in mind but begin with understanding and developing concepts is at the heart of the common core. 
This shift in standards does not guarantee a shift in learning, this will only happen when teachers change the way they teach and curriculum evolves from focusing on some learners, to all learners in the classroom. From gifted and talented to students with special needs and English language learners, our approach and modes of instruction need to be flexible and supportive of our classroom population. Students need a variety of pedagogical approaches from number talks that support discussions of strategies and mental calculations, to manipulatives (virtual, concrete, and student-created) that allow students to construct models and make meaning of concepts.
So when parents ask, “Why can’t they just memorize their multiplication facts” we can assure them that memorization does not promote understanding and automaticity will develop with practice. Elementary teachers should begin introducing concepts by building on what children already know and albeit this may be intuitive, it can lead to a deeper understanding of the concepts.
Rooting math in the lives of the students we teach can support building conceptual understanding as well as transfer the learning of math (number words, symbols and quantities) into their informal learning experiences such as the park, playing games and with friends. Take for example the idea of using arrays to introduce the concept of multiplication. Arrays are all around students but this knowledge needs to be brought forward during instruction and through practice. It’s not enough just to talk about where you might see arrays kids also need to construct , discover, apply and identify. We should understand that what works for one kind of learner might not work for another.
Woodward and Baxter found that students with disabilities in math tend to make significantly less growth in discussion-oriented classes (1997) than traditional ones. This findings suggests just because conversations are happening does not mean learning is occurring.
Technology can be a great mediator to support, and challenge students with open ended tasks and flexibility. It can also be useful to move from the abstract to the real-life connection.
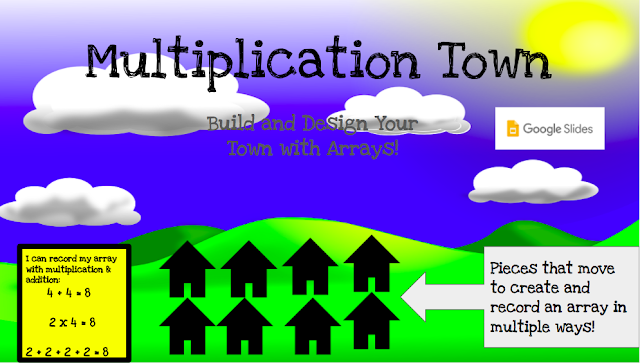 |
| Available as a Google Slide here |
Repeated addition is the knowledge students can start with to build an understanding of multiplication, but some students in your class might not have developed automaticity of their addition facts. Working with arrays that are highly contextualized and not just on a piece of graph paper can provide practice in addition while also introducing the concept of multiplication. In this video a second-grader works on a Google Slide presentation his teacher made to drag and drop cars into a parking lot. If our ancestors first counting tool was their fingers then digital devices might be consider the cultural tools for our students today. 
Using this digital lesson teachers can scaffold instruction and allow students to work at their own pace. While some students might work with benchmark numbers 2’s, 5’s, and 10’s to construct an array, students who understand the concept of multiplication and have strong number sense in this area can move to more complex equations.
Are you using technology to support students conceptual understanding in your math class? Share your ideas here and join the conversation on our Facebook Group! Don’t forget to check out my list of digital tools and add your favorites as well.





